实模态和复模态的区别与联系

实模态和复模态是模态分析中的两个重要概念，它们在振动系统的动态特性描述中具有显著的区别与联系。

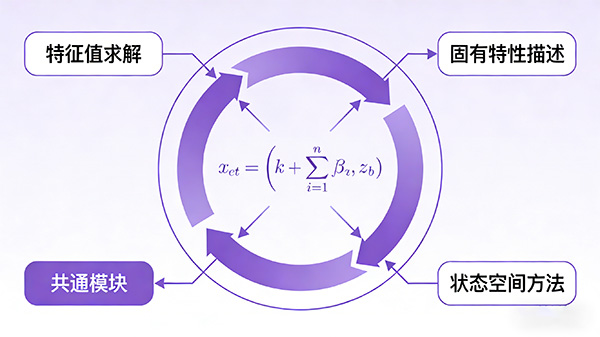
以下是对实模态和复模态的区别与联系的详细归纳：

一、定义与特性

实模态：

定义：实模态是指振动系统的模态矢量(模态振型)是实数矢量的模态。

在无阻尼或比例阻尼(即阻尼与系统的质量和/或刚度成比例)的情况下，系统的模态矢量是实数，此时称为实模态。

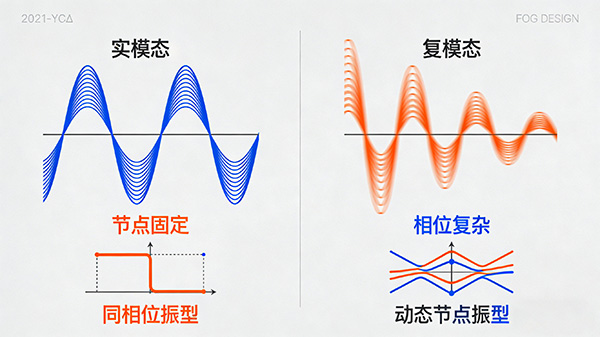
特性：实模态振型上各点的相位相同或相差180度，节点位置固定不变。

系统的振动特性可以用实数来描述，如固有频率、模态质量、模态刚度等。

复模态：

定义：复模态是指振动系统的模态矢量是复矢量(即包含实部和虚部)的模态。

在非比例阻尼(即阻尼与系统的质量和/或刚度不成比例)的情况下，系统的模态矢量是复数，此时称为复模态。

特性：复模态振型上各点的相位关系复杂，不再保持同相位或反相位的关系，节点位置也可能随时间变化。

系统的振动特性需要用复数来描述，如复频率、复模态质量、复模态刚度等。

二、数学描述与求解

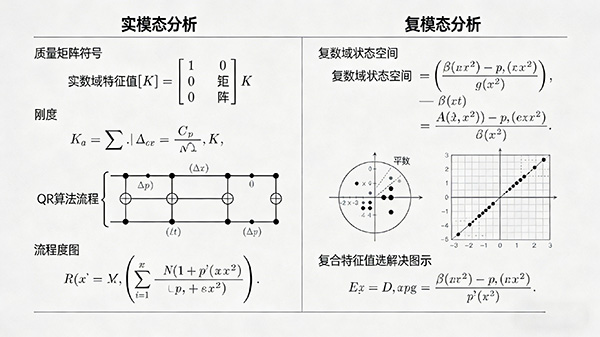
实模态： 在无阻尼或比例阻尼系统中，系统的运动方程可以简化为实数域内的特征值问题。

通过求解系统的质量矩阵、刚度矩阵和阻尼矩阵的特征值，可以得到系统的固有频率和模态振型，它们都是实数。

实模态分析通常使用标准的特征值求解方法，如QR算法、Lanczos算法等。

复模态： 在非比例阻尼系统中，系统的运动方程需要在复数域内求解。

由于阻尼矩阵的非对称性，系统的特征值和特征矢量都是复数。

复模态分析通常使用状态空间方法或复特征值求解技术。

状态空间方法通过引入状态向量将系统的运动方程转化为状态空间方程，然后在复数域内求解状态空间方程的特征值。

三、应用与意义

实模态： 实模态分析在结构动力学、机械振动、声学等领域有广泛应用。

它可以帮助工程师了解结构的固有振动特性，预测结构的动态响应，优化设计结构参数等。

实模态分析的结果对于结构的故障诊断、振动控制、噪声抑制等方面具有重要意义。

复模态： 复模态分析在涉及非比例阻尼的复杂振动系统中具有独特优势。

它可以更准确地描述系统的振动特性，特别是在高频振动、非线性振动和复杂结构系统中。

复模态分析的结果对于结构的精确建模、动态特性预测、振动控制策略设计等方面具有重要意义。

四、联系

数学基础：实模态和复模态都基于线性振动理论，通过求解系统的特征值和特征矢量来描述系统的振动特性。

物理意义：无论是实模态还是复模态，它们都反映了振动系统的固有特性。

实模态描述了系统在无阻尼或比例阻尼下的振动形态，而复模态则描述了系统在非比例阻尼下的振动形态。

分析方法：实模态和复模态的分析方法在某些方面可以相互借鉴。

例如，状态空间方法既可以用于复模态分析，也可以在某些情况下用于实模态分析。

综上所述，实模态和复模态在定义、特性、数学描述、应用与意义等方面存在显著的区别与联系。

在实际应用中，需要根据具体问题和需求选择合适的模态分析方法。